在接下来的文章中，我将论证反粒子在自然界中存在需要的两个条件：一是粒子的能量总是正的，二是自然界遵循相对论原理。

时空图！

为了充分把握本文的结论，需要对时空图（或闵可夫斯基图）的几何性质进行解释。时空图是粒子在时空中运动的图示。

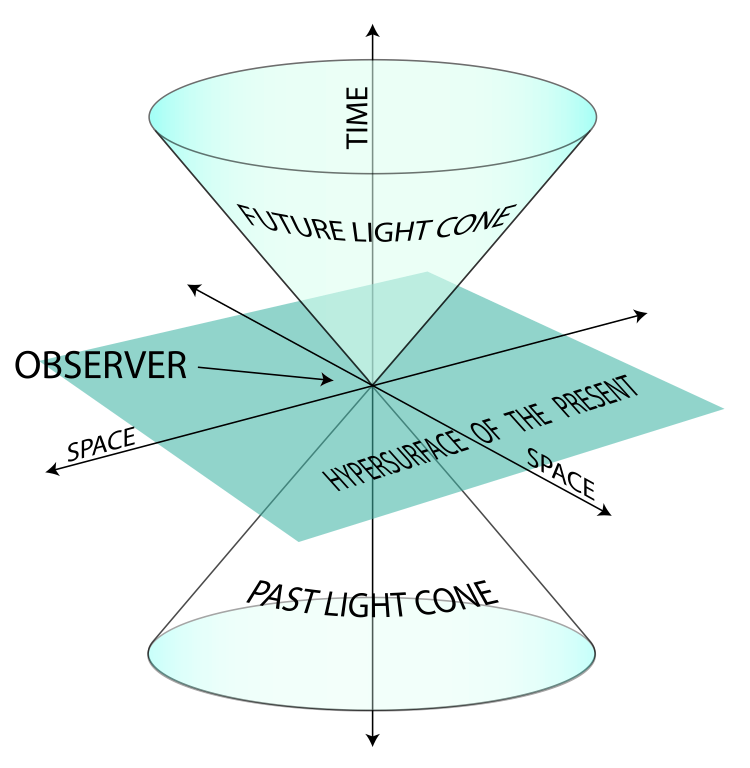
图1：二维光锥（维基百科）。

为了更好地理解：

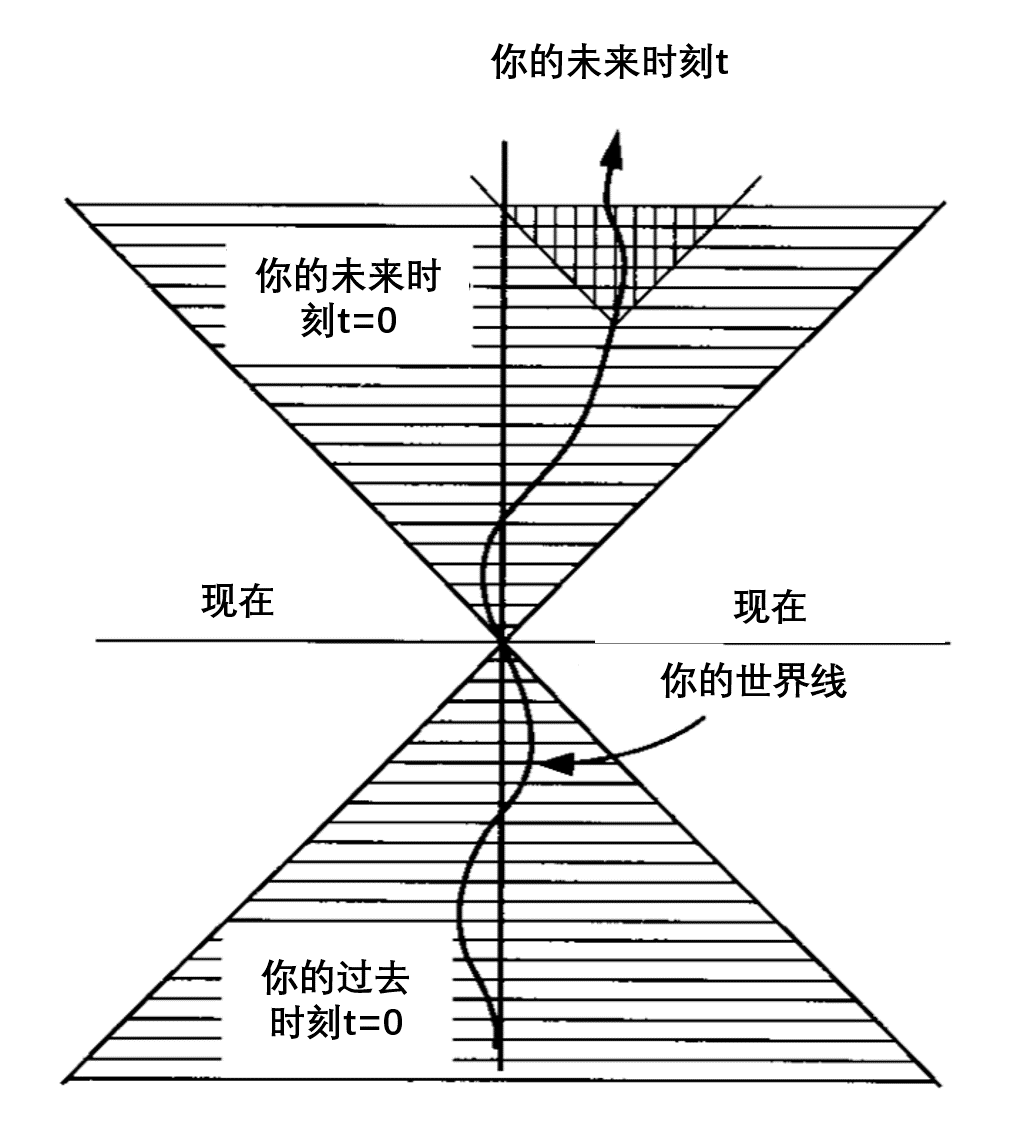
图2：2维闵可夫斯基图描述的是在一个空间维度和一个时间维度的宇宙中发生的事件。

在闵可夫斯基图中，速度是曲线斜率的倒数。一个光子以光速v=c运动，一条45度的线可以描述它（为了方便起见，我们选择c=1）。一个观察者以恒定的中间速度在零（垂直线代表静止的粒子）和光速之间移动，它在一条中间斜率的线上移动。其他类型的世界线的斜率不能小于1，这就将它们限制在图2中两条45度线边界的区域。观察者不能进入楔形之外的区域（形成一个楔子）。如果在这个外部区域有两个事件相互影响，它们之间的信息将比光更快，而且会违反因果关系，因为事件的顺序会根据参照系而改变。稍后将更详细地讨论这一点。

反粒子是什么？

自然界的每一种粒子都有其相应的反粒子。反粒子的质量与其伴随粒子（associated particle）相同，但电荷相反。反粒子最著名的例子是带正电荷的正电子（或反电子）。正电子是与带负电荷的电子相联系的反粒子。大多数标准的量子场论书籍都以同样的方式定义反粒子。这篇文章，我将运用兰卡斯特和布伦德尔（ Lancaster and Blundell’s ）的方法。

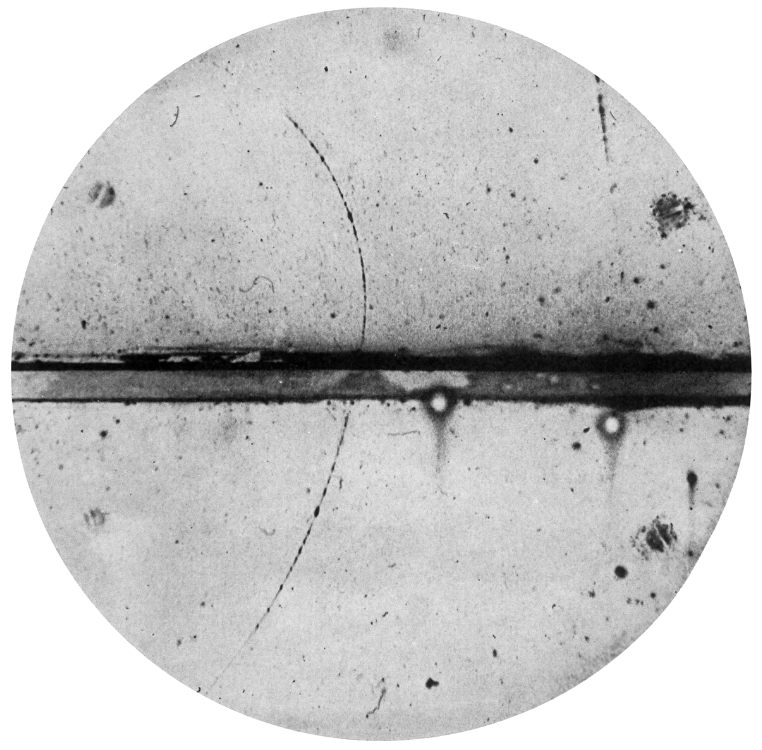
图3：观察到的第一个正电子（向上的曲线）。正电子进入左下方的腔室，被引线（粗粗的水平线）减慢，被外加磁场弯曲，然后向左上方弯曲。

费曼-施塔克尔伯格：时间上向后移动的粒子

20世纪40年代，理查德·费曼（Richard Feynman）和恩斯特·施塔克尔伯格（Ernst Stuckelberg）提出了将具有负能量的状态视为时间倒退的粒子的概念。我们现在称这些粒子为反粒子。例如，在运动方程中，一个带电粒子在电磁场中：

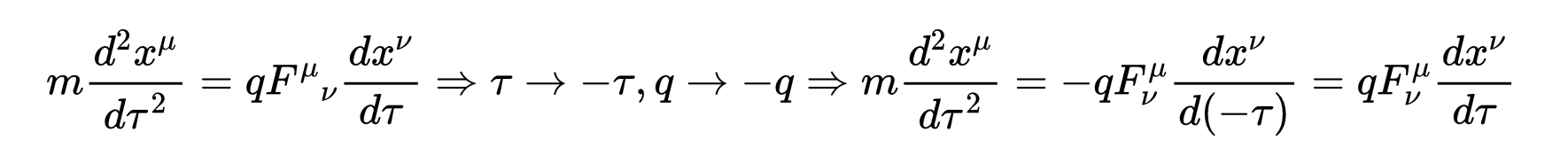
式1：如果电磁场中一个带电粒子的运动方程改变了时间和电荷的符号，方程保持不变。

改变时间的符号，我们马上就能看到它的效果和反电荷是一样的。这意味着一个向后移动的粒子看起来就像一个带相反电荷的反粒子在时间上向前移动。

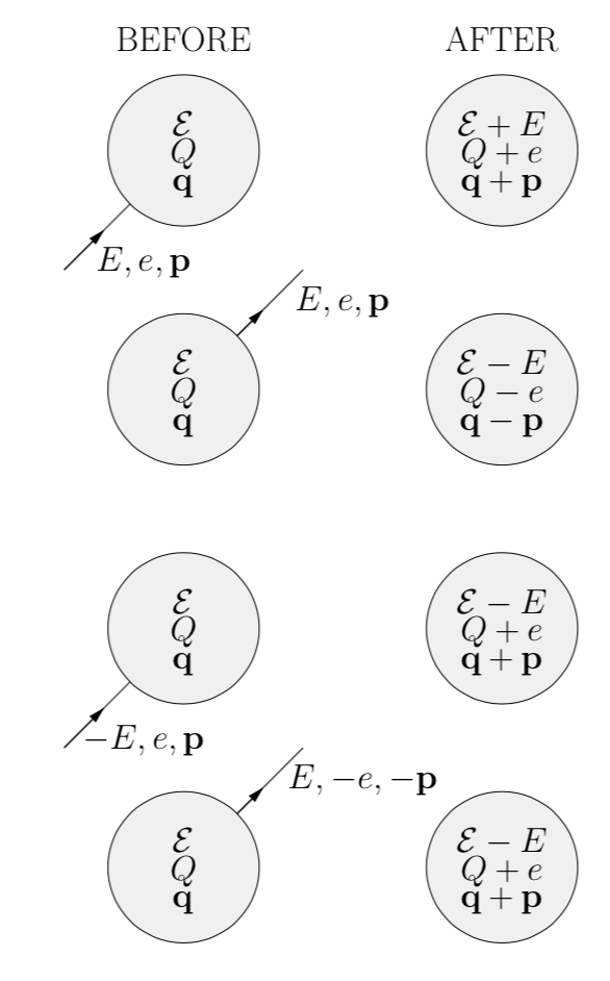
图4：在正文中描述的等价性（图片来源：《天才业余爱好者的量子场论》）。

让我简单地提一下所谓的CPT定理（电荷、奇偶性和时间反转对称），这是一个所有物理现象都遵循的基本对称性。CPT分别表示电荷C，奇偶性P和时间反转T。根据该定理，电荷共轭，奇偶性变换，时间反转时，物理定律不变。在本例中，我们可以忽略P，关注C和T。另一种解释反粒子的方法是说它是CT对称的。

量子力学中的微扰理论

让我们考虑一个粒子在某初始状态下：

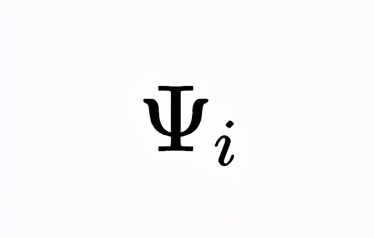
在量子力学中，跃迁振幅和粒子跃迁的概率：

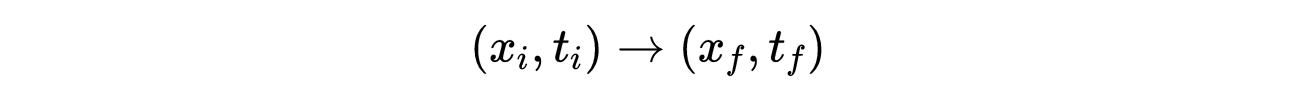
式2：空间和时间中从初始点到最终点的过渡。

分别为：

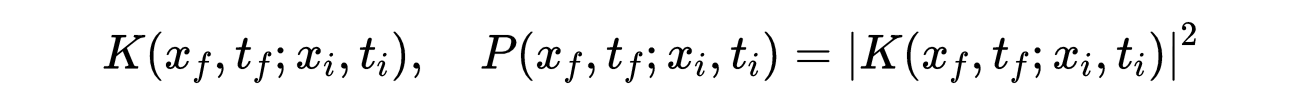
式3：式2中概率幅值和相应的跃迁概率。

其中K被称为传播子。与传播器对应的格林函数为：

式4：对应于式3中的传播子的格林函数。因果关系通过Θ函数构建到格林函数中。

注意，因果关系是通过Θ函数构建到格林函数中，如果其参数为负（如果最终时间大于初始时间），则该函数为零。

如果系统是时间平移不变的，则传播子只依赖于时间差t−t ‘。自由格林函数G_0为：

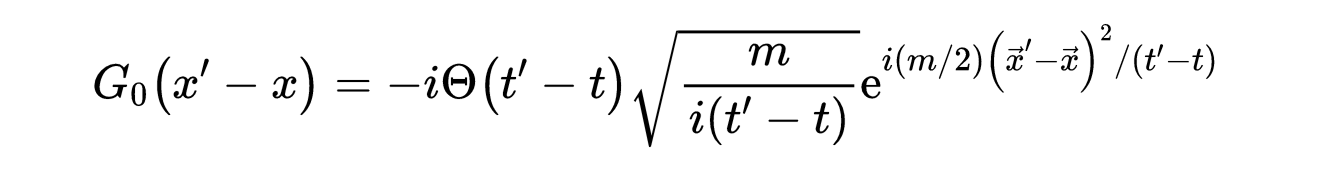
式5：位置空间中自由格林函数G_0

图5：粒子从ψ_i到ψ_i，无相互作用。

上图描述了如下转换：

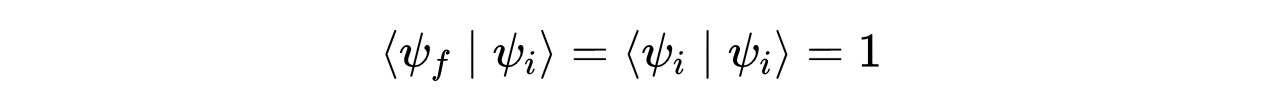
ψ_i→ψ_i的非相互作用粒子的跃迁振幅为1（什么也没有发生）。

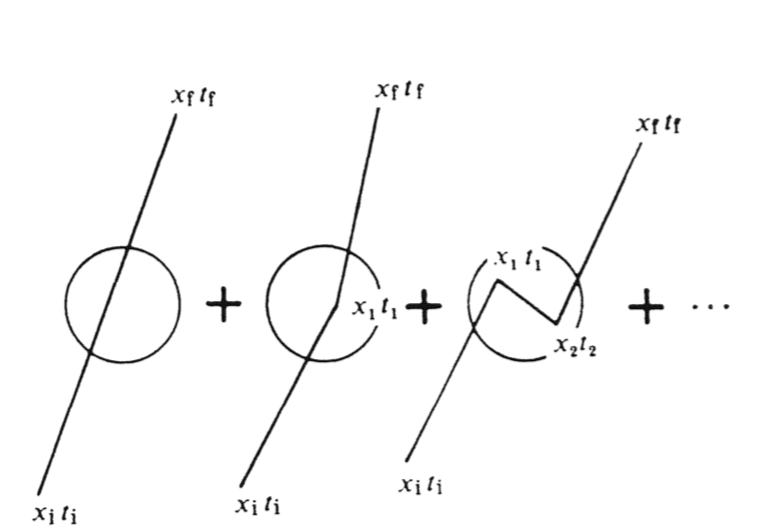
图6：扰动序列。

一个粒子对另一个粒子的散射用与势V(x,t)的相互作用来描述。在相互作用存在的情况下，跃迁振幅或格林函数不能精确地计算出来。然后使用微扰展开法（适用于小的势能V）：

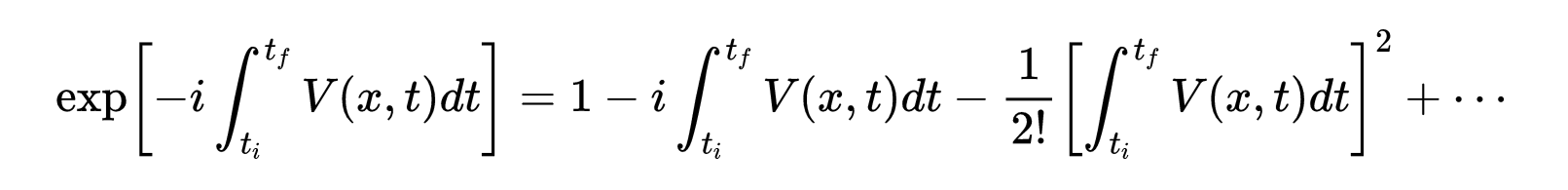
式7：微扰展开，适用于小V。

现在，格林的函数G_0可以表示为动量空间中的积分：

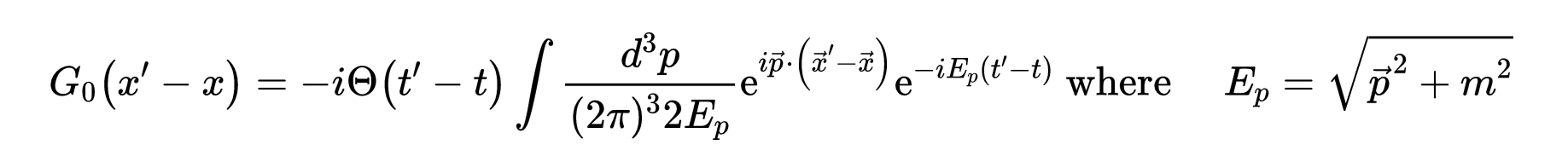
式8：自由格林函数G_0表示为动量空间的积分。

两次作用

现在假设粒子与势V(x,t)相互作用两次，分别在x_1和x_2点。为简单起见，让我们用x表示(x,t)。为了求得初始状态ψ_i的振幅，并在两次相互作用后返回到状态ψ_i。根据费曼的方法，写出粒子所遵循的三个步骤，即：

首先，初始态ψ_i下的粒子在x_i与V相互作用，并将其置于中间态m，能量为E(m)。
对于时间t_2 – t_1，粒子从x_1→x_2自由演化，。与此步骤相关的自由格林函数由式5或式8给出。在这一步中，所有可能的中间态m被求和。
第二次与V在x_2的相互作用将状态转换回初始状态ψ_i。

我们得到：

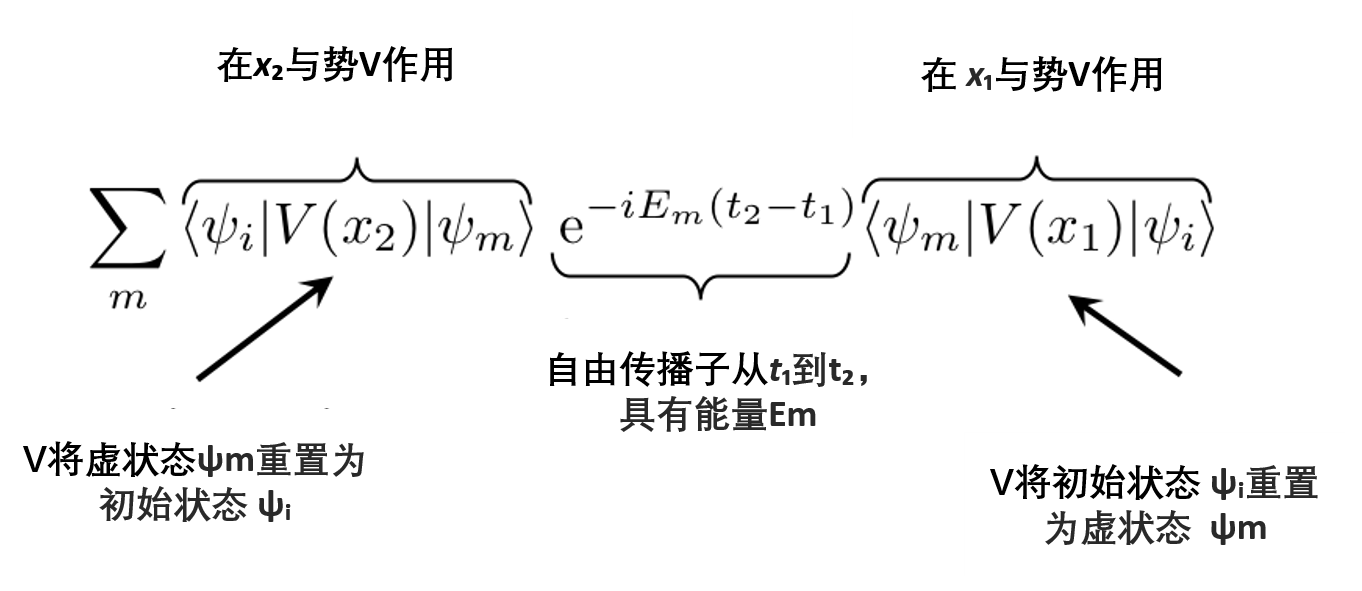
式9：ψ_i→ψ_i返回的振幅是势的二次型。

将中间状态设为平面波，式9可以写成：

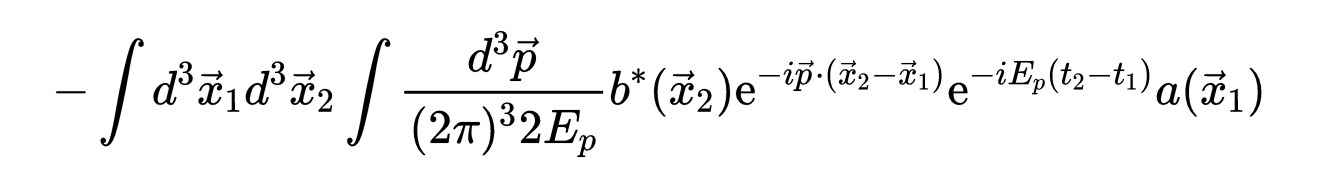
式10：用平面波作为中间态的式9。

因子a和b表示：

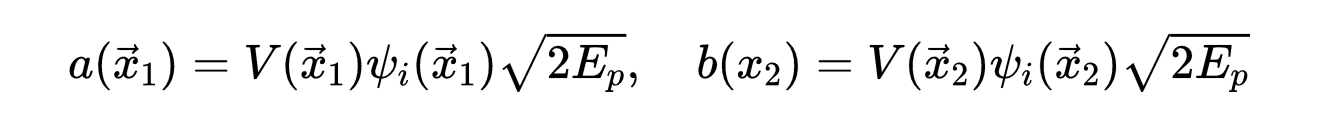
式11：式10中的因子a和因子b。

其中能量如式8所示。因此，中间态是动量p和能量E(p)的粒子。下图说明了这个过程：

图7

因为我们感兴趣的是粒子回到初始状态的概率，我们将式6给出的直接跃迁的振幅与式10给出的V²散射的振幅相加，然后将结果平方。概率为：

式12

傅里叶变换

函数f(τ)的傅里叶变换等于它分解成组成频率ω（注意傅里叶变换不限于变量t和ω）。傅里叶变换的输出是ω的复函数。它的模量表示原始函数f(τ)中每个频率的量。傅里叶反变换将原始函数f(τ)从其频域表示中合成出来。从数学上讲，傅里叶变换及其逆是这样的：

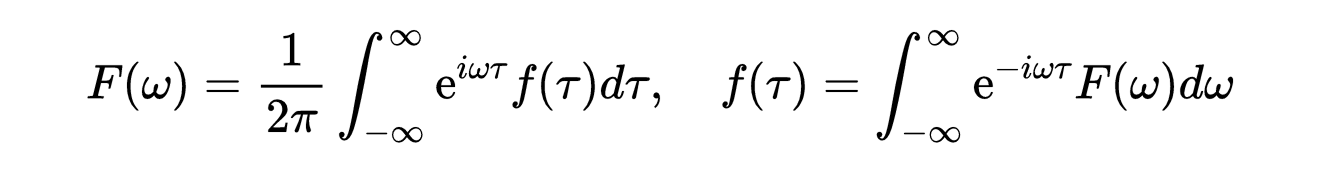
式13：时频傅里叶变换及其逆的定义

下图说明了从时间到频率的傅里叶变换。

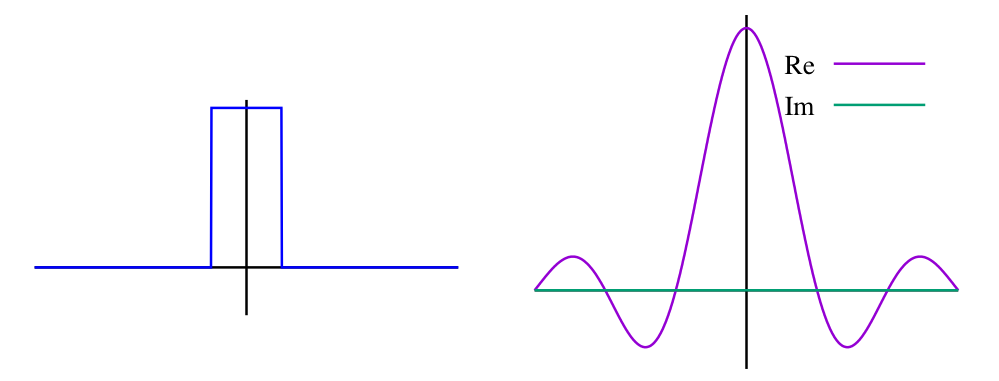
图8：单位脉冲函数（t的函数）的傅里叶变换和它的傅里叶变换（ω的函数）。

反粒子的必然性

为了证明反粒子的必然性，我们假设所有的能量都是正的。然后将公式12中的动量积分变换为：

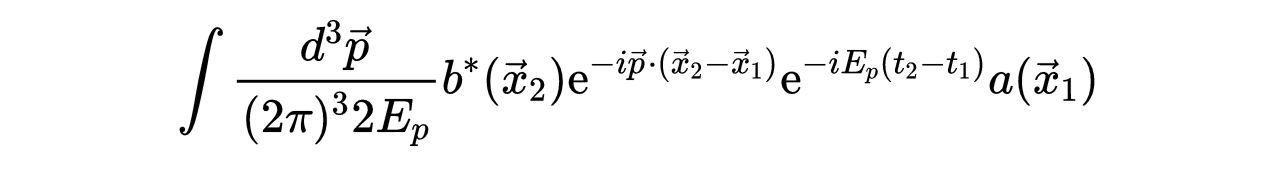
式14：方程式12中的动量积分。

将其转化为对能量ω=E(p)的积分，并定义一个函数F(ω)，对于ω < m，使F(ω)=0。注意，F(ω)中包含x_1，x_2依赖关系。

图9：函数F(ω)。

式14就变成：

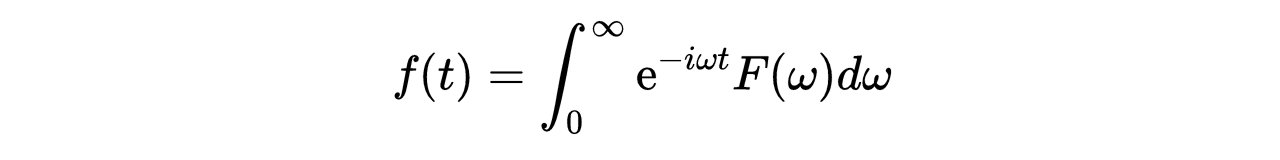
式15：仅包含正频率的傅里叶分解函数。

根据费曼的理论，考虑下面的定理。如果函数f(t)只能分解成正频率，根据这个定理，F (t)不可能在任何有限的时间范围内为零。

现在让我们把这个定理应用到我们现在的情况。首先，确定空间坐标x_1和x_2，并考虑基于ω的动量积分。

但对于一个固定的x_1，当第二坐标x_2位于x的光锥之外时，动量积分式14不可能等于0。我们得出结论，式14必须包含包含类空间间隔（粒子运动速度超过光速）的非零振幅。

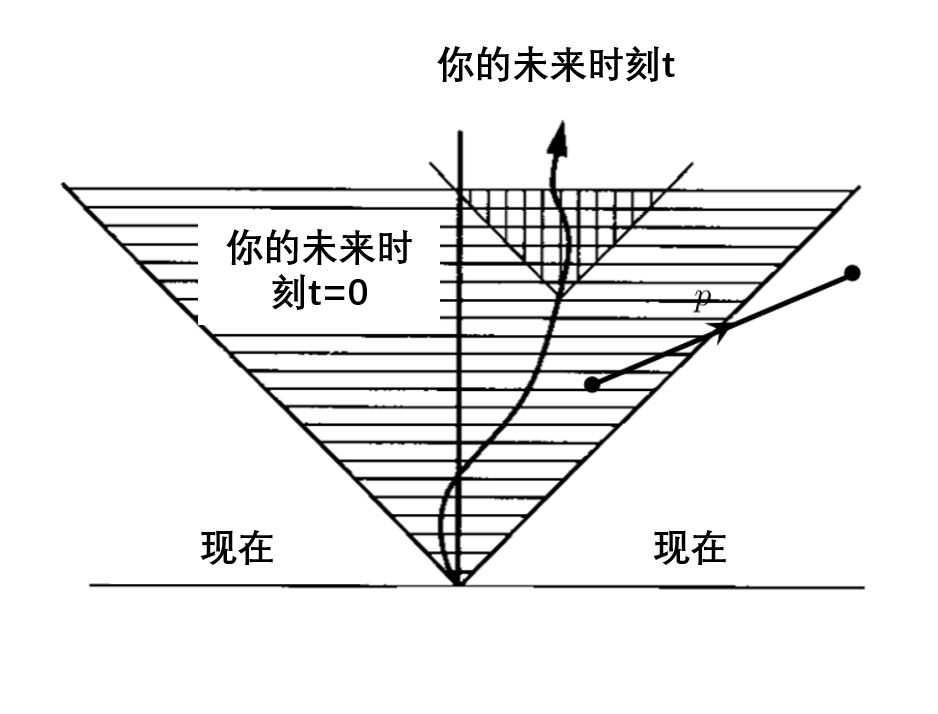
图10：具有类似空间间隔的光锥

但正如我们在前面所解释的，类空间间隔具有与框架相关的事件顺序。因此，一些中间粒子在另一个参照系中被看作是“在时间上向后传播的粒子”。现在，让我们给粒子加一个电荷。如上所述，根据费曼-施图克尔伯格的解释，这些在时间上向后移动的中间粒子与在时间上向前移动的反粒子是等价的！

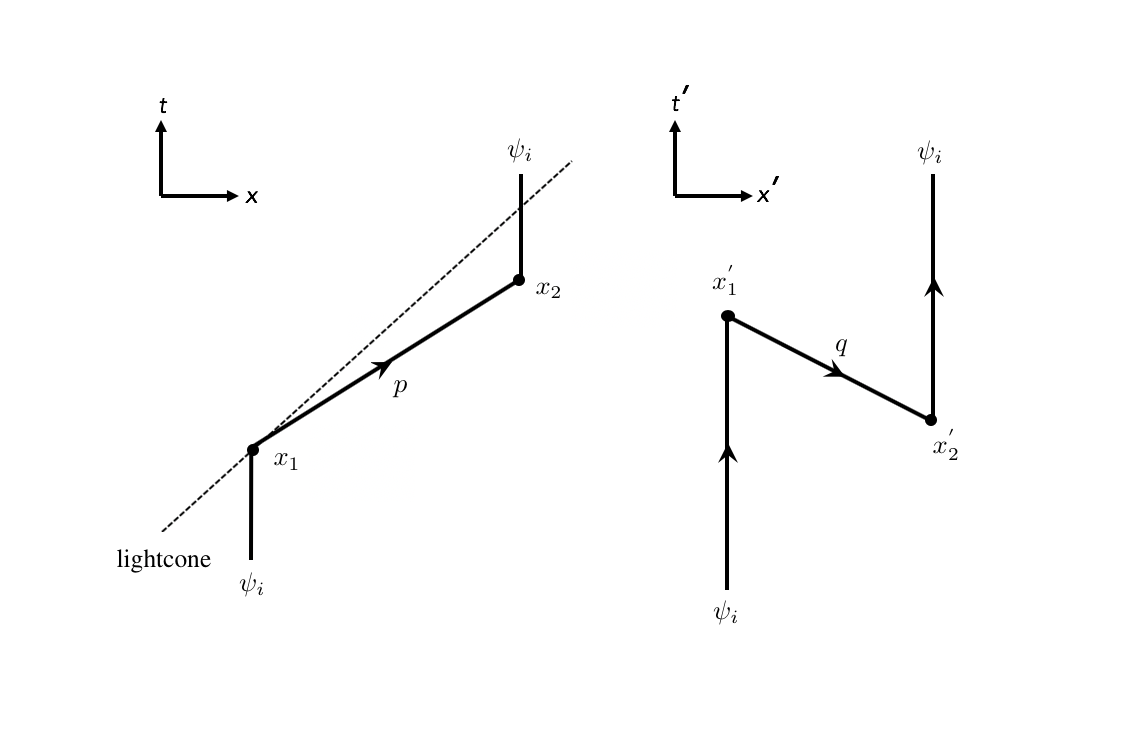
图11：光锥内外运动的必然性。

为了使论点更清楚，让我们仔细研究图11。假设我们转换成一个新的参考系，其中t_2< t_1。让我们看看会发生什么。在新的参照系中，只有一个运动粒子ψ_i，直到t=t_2，。然而，在t_2势V创造了两个粒子，其中一个似乎在时间上向后移动。然后在t_1处原始粒子和向后移动的粒子相遇并消失。换句话说，这两个粒子在新的参考系中相互湮灭。