虫洞是爱因斯坦引力理论中的场方程的解，它类似于永恒黑洞内部两个相同宇宙之间的隧道，或时空中两个遥远的点之间的隧道。通过虫洞，人们可以缩短巨大的空间和时间距离。原则上，虫洞可以用于空间旅行，甚至可以旅行到过去。然而，虫洞通常是不稳定的结构，而且它们的存在仍然是一个悬而未决的问题。

“虫洞”这个名字是由美国著名物理学家约翰·惠勒（他也发明了“黑洞”这个名字）创造的。

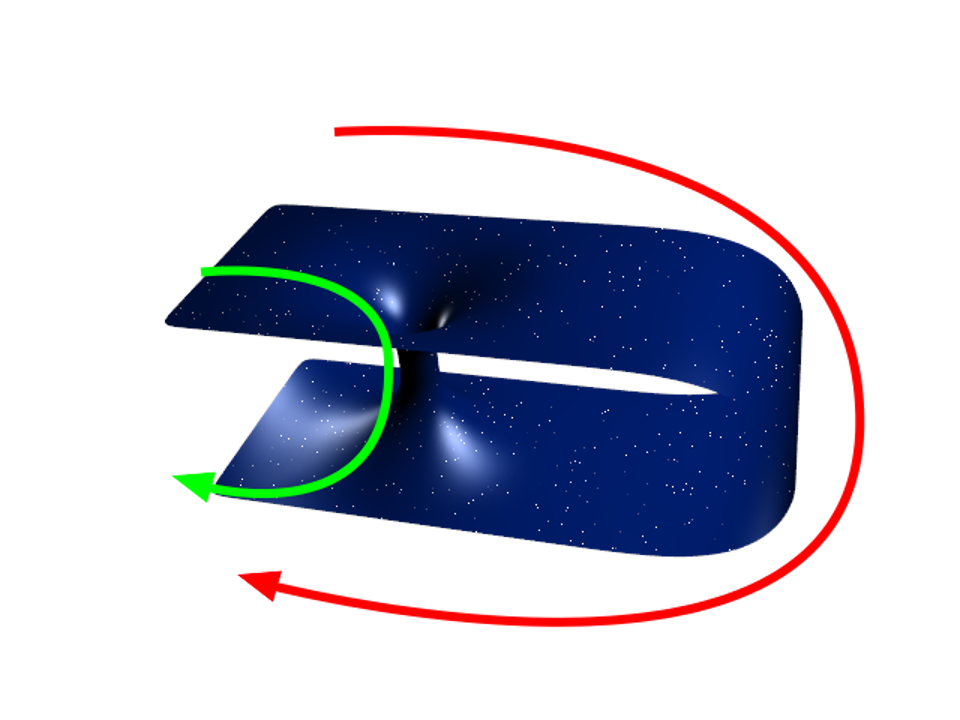
• 图1：二维的虫洞

第一种虫洞是由奥地利物理学家路德维希·弗拉姆（Ludwig Flamm）发现的。这一发现发表在他1916年的论文《爱因斯坦引力理论评论》中。

• 图2：路德维希·弗拉姆和他1916年的论文《爱因斯坦引力理论评论》

​1935年，阿尔伯特·爱因斯坦和美国-以色列物理学家内森·罗森（Nathan Rosen）重新发现了弗拉姆虫洞（这就是这种类型的虫洞通常被称为“爱因斯坦-罗森桥”的原因）。

• 图3：罗森和爱因斯坦以及他们著名的论文。

黑洞及其几何学

在静态黑洞附近，时空度规变成了所谓的史瓦西度规：

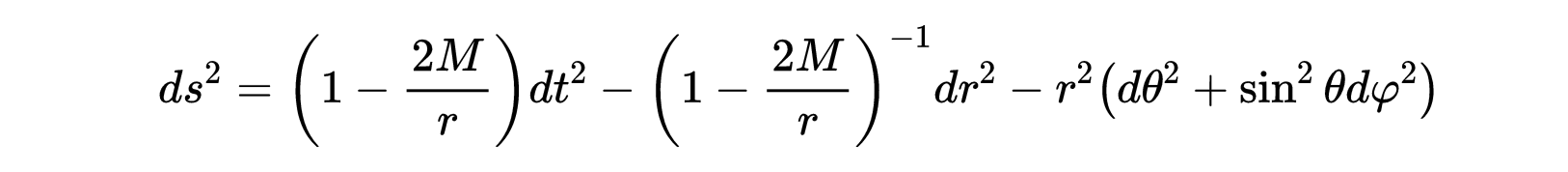
• 式1：史瓦西或静态黑洞的线元素。

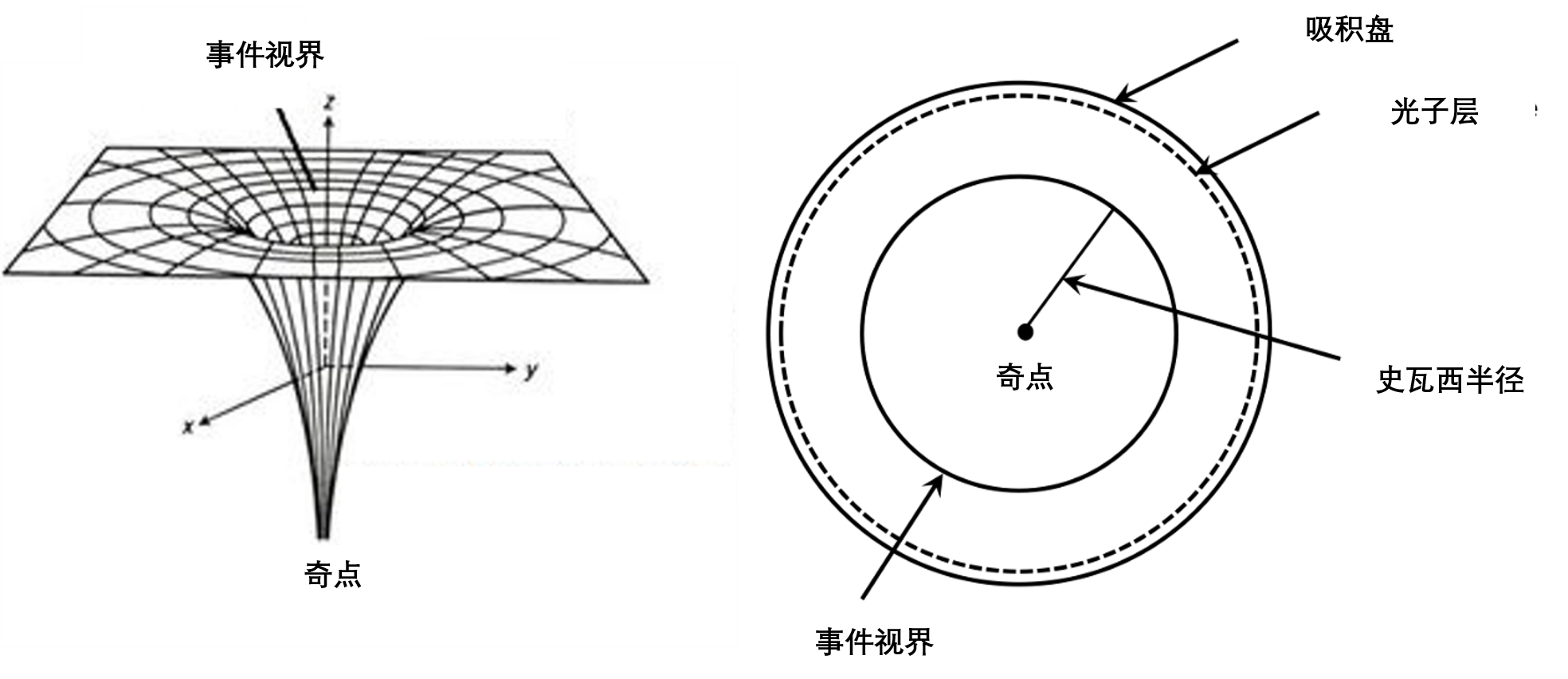
• 图4：图中右侧的史瓦西黑洞有一个吸积盘（由围绕中心天体的弥散物质形成）。在所谓的光子层中，重力场迫使光子在轨道上运动。

线元素用球坐标表示：

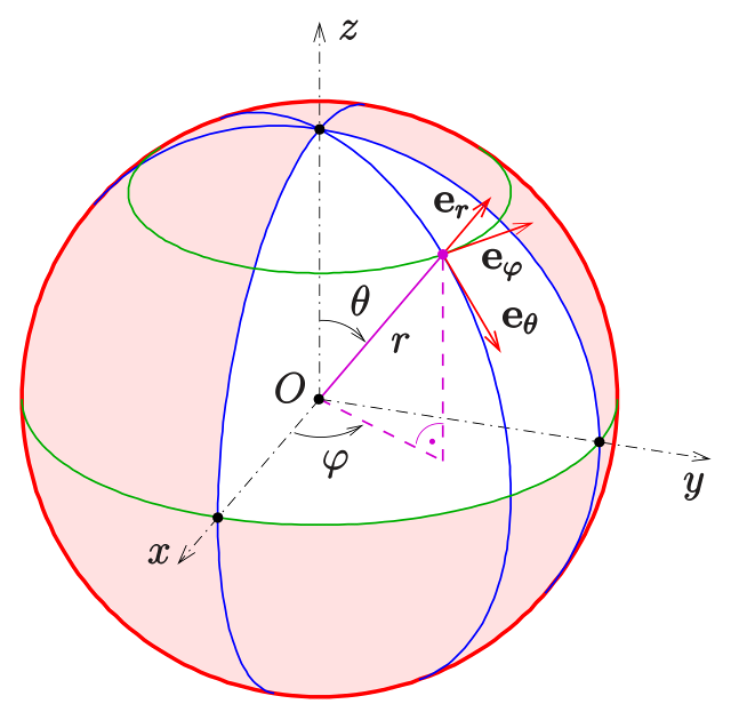
• 图5：球面坐标(r， θ， ϕ)

现在考虑以下新的坐标集：

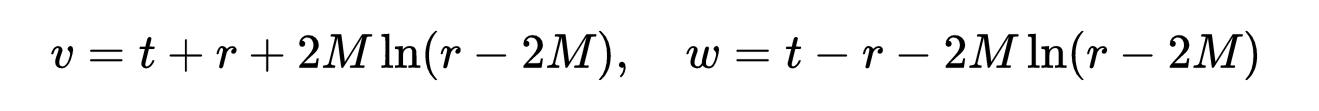
• 式2：提前和延迟零坐标

如果我们固定角坐标θ和φ并将史瓦西度规写成v和w的形式，我们得到：

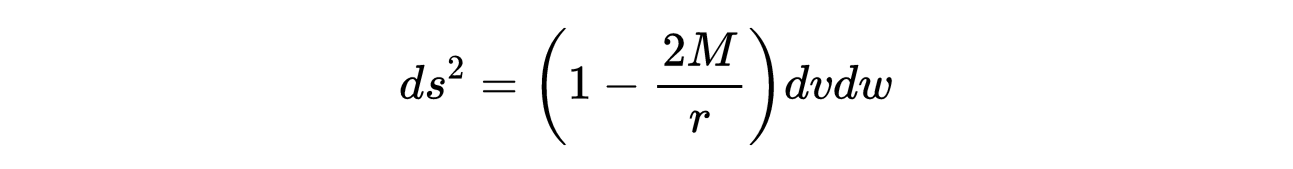
• 式3：θ =常数和φ=常数的史瓦西度规用提前和延迟零坐标表示。

与式3对应的度规被认为是保角平坦的。为了理解这意味着什么，考虑以下对克鲁斯卡尔变量（Kruskal variables）的转换：

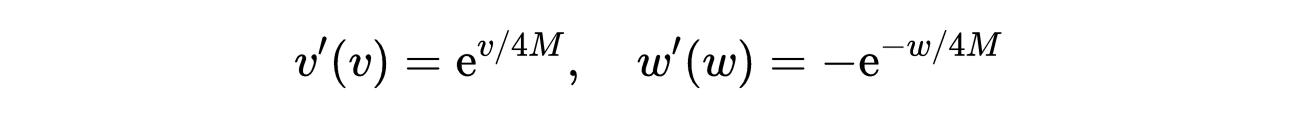
• 式4：克鲁斯卡尔坐标变换。

​克鲁斯卡尔坐标变换是保角变换的一个例子，保角变换是局部保角的映射。

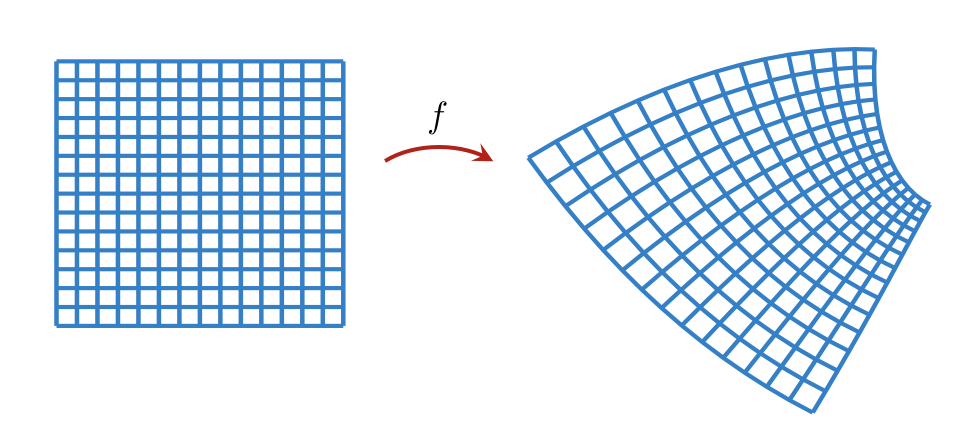
• 图6：局部保角的保角变换的图解。

引入以下“时间”和“空间”坐标：

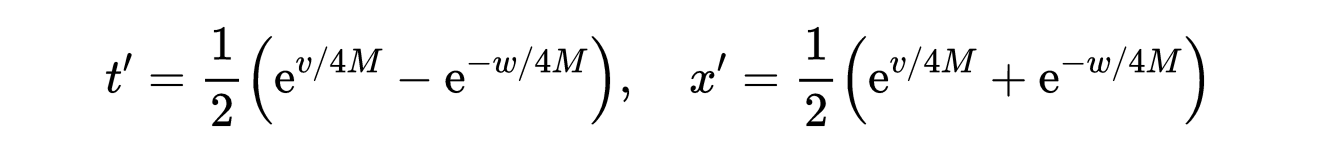
• 式5：用克鲁斯卡尔坐标表示的新“时间”和“空间”变量。

史瓦西度规变成：

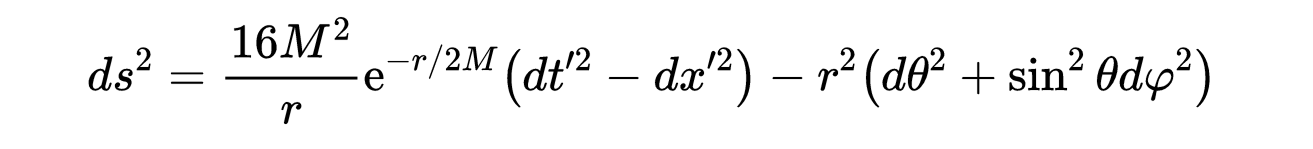
• 式6：史瓦西黑洞的线元素用x ‘和t ‘表示，r是x ‘和t ‘的函数。

其中r对式6中变量的依赖关系为：

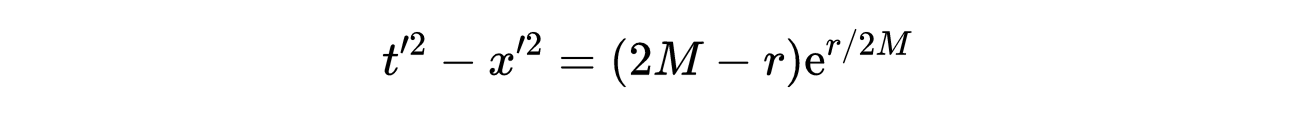
• 式7：由式6得到r，x ‘，t ‘之间的关系。

有以下的解：

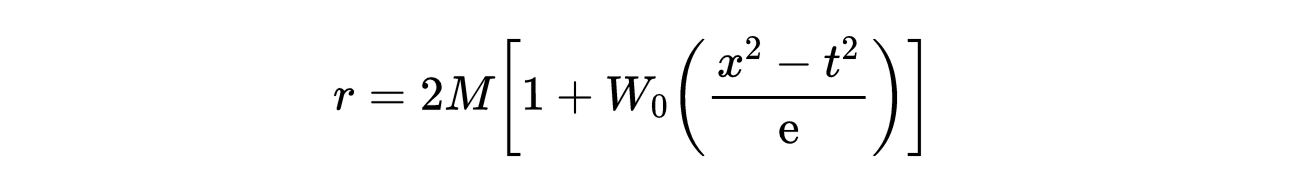
• 式8：方程7中r的解

其中W_0是朗伯函数的主要分支。在式6中，如果我们固定角变量θ和φ，我们就得到了平坦时空的线元，这叫做保角平坦。

Kruskal-Szekeres图

带有(θ， φ)常数的Kruskal-Szekeres图如图7所示。它具有以下特性：

• 径向零测地线是直线
• 曲线r =常数是由式7给出的双曲线。对于每个r，我们有两条曲线（实际上是超曲面，因为(θ， φ)从图中被省略）。特别地，有两个奇点对应于r = 0处，一个在过去，一个在未来。
• 我们可以看到一个粒子离开点(r,t ‘) = (4m, 0)，穿过视界(r = 2M)，落入奇点(r = 0)。
• 从观测者发出的信号沿着上述测地线逃逸到无穷远，除非它们被发射到事件视界之外。否则，他们就会被困在里面。
• 这个图分为四个区域：黑洞内部(II)，白洞内部(II’)，以及两个外部区域(I和I’)。
• 实际上，图中的每一点都是一个带度规的二维球体：

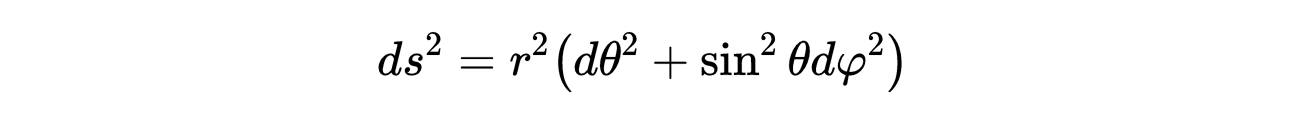
• 式9：Kruskal图中每个点的几何形状，这是一个二维球体。

• 图7：Kruskal图。这四个象限是黑洞内部(II)，白洞内部(II’)和两个外部区域(I和I’)

爱因斯坦-罗森桥

让我们考虑超曲面t ‘ =0（回想一下，Kruskal图中的每个点都是一个二维球体）。这个超曲面（如式6和式8所示）上的线元素为：

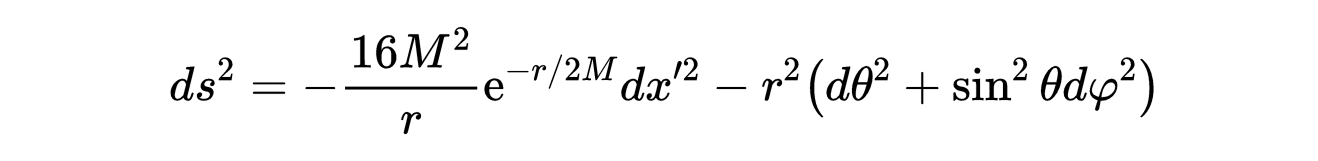
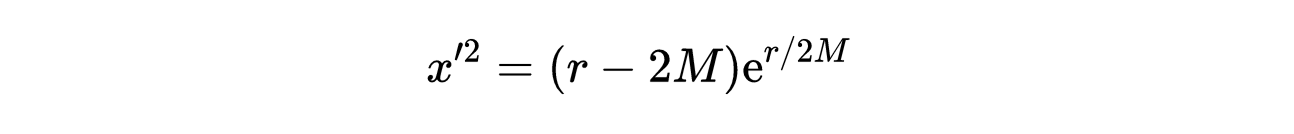
• 式10：t ‘ =0时，式6和式8中给出的超曲面的线元素。

​r的第二个方程解为：

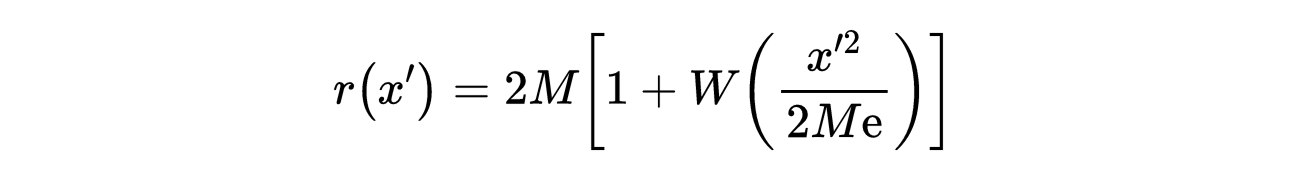
• 式11：式10中第二个方程的解。

​其中W是朗伯函数。当x ‘从正无穷到负无穷时，上述函数减小到最小半径r = 2M，出现在x ‘ =0处。

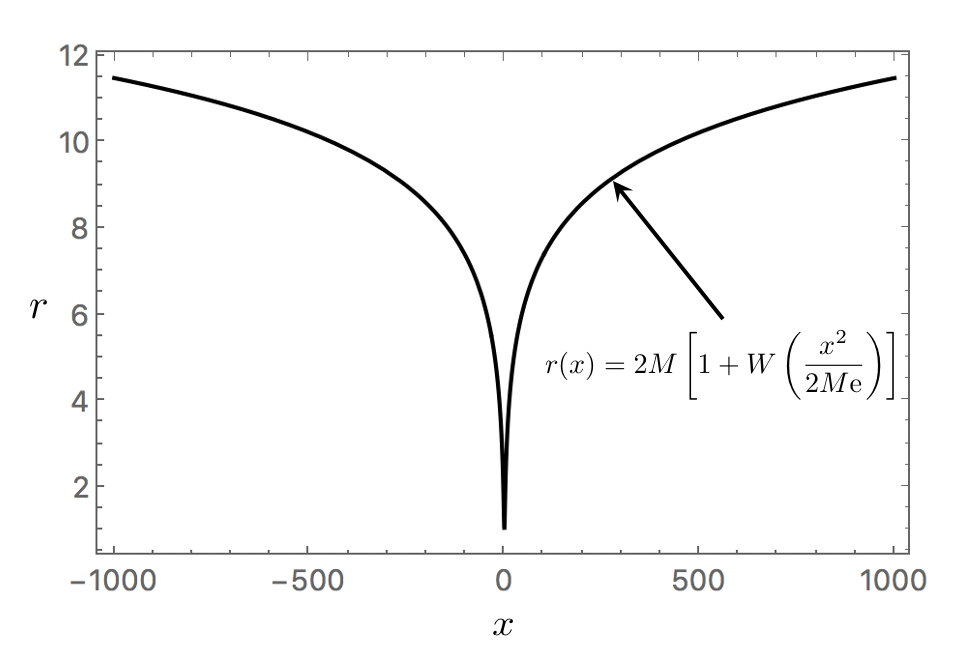
• 图8：设2M=1时式11的曲线图。

​既然图中的每个点都是二维球面，我们可以选择一个截面θ = π/2。如图5所示，这个横截面就是赤道面。这个指标简化为:

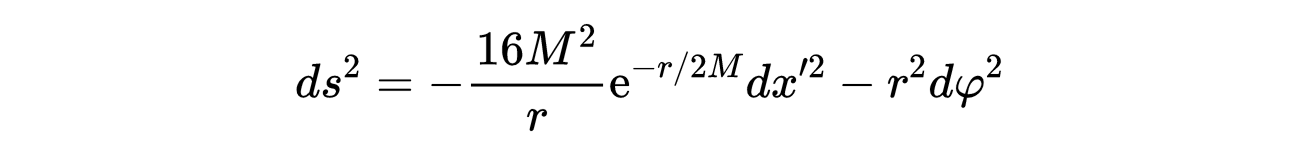
• 式12：θ = π/2的式10中的度规。

​我们可以通过以下方式更好地理解这个度规。考虑一个嵌入三维平面空间的线元方程12的二维曲面。它看起来如下图所示。

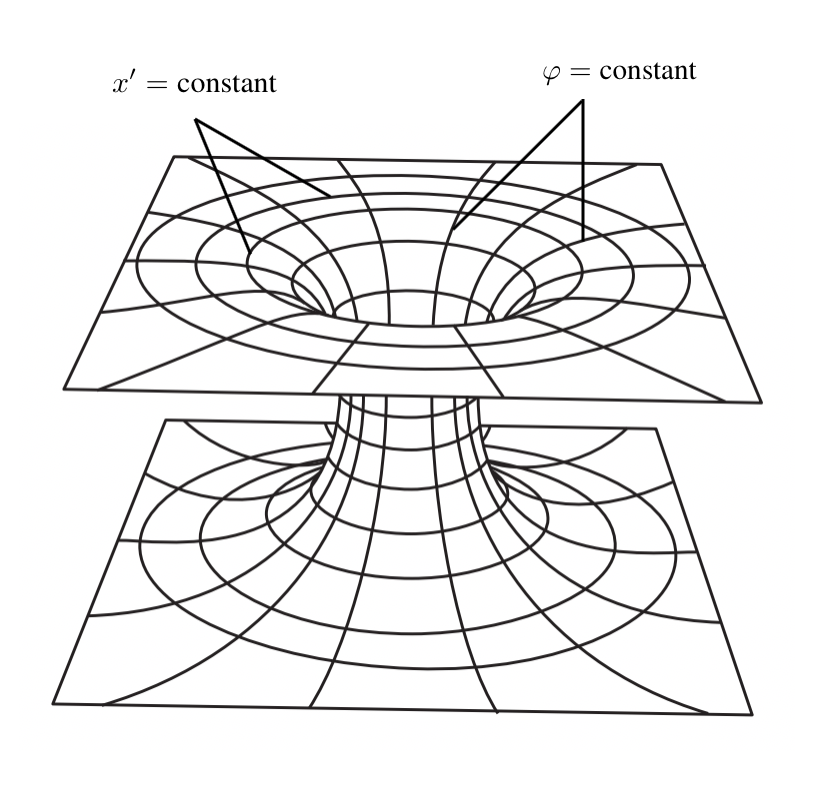
• 图9：嵌在三维平面空间中的线元由式12给出的二维曲面。

​正如前面提到的，当t ‘ =0保持不变并沿x ‘移动时，我们发现在x ‘ =0点对应的球面半径是最小的（r=2M）。这是连接两个宇宙的史瓦西流形的“咽喉”。这个解不限于t ‘ =0。随着我们改变“喉道”的半径，直到它闭合，将两个宇宙彼此隔开（图10）。这个度规描述了爱因斯坦-罗森桥或史瓦西虫洞。

• 图10

与Kruskal图相对应的解被认为是一个极大扩展的解，与一个典型的黑洞的解是不同的，这是一个恒星坍塌的结果。后者的图既不包含白洞，也不包含对应于另一个宇宙的区域。这个新宇宙在最大扩展解中的真实存在仍然是一个悬而未决的问题。

广义相对论的爱因斯坦场方程是局部的。这意味着它们不能决定时空的整体几何性质。解方程10可以嵌入不同拓扑的时空中。下面图11中的例子显示了一个连接两个遥远时空区域的史瓦西虫洞。

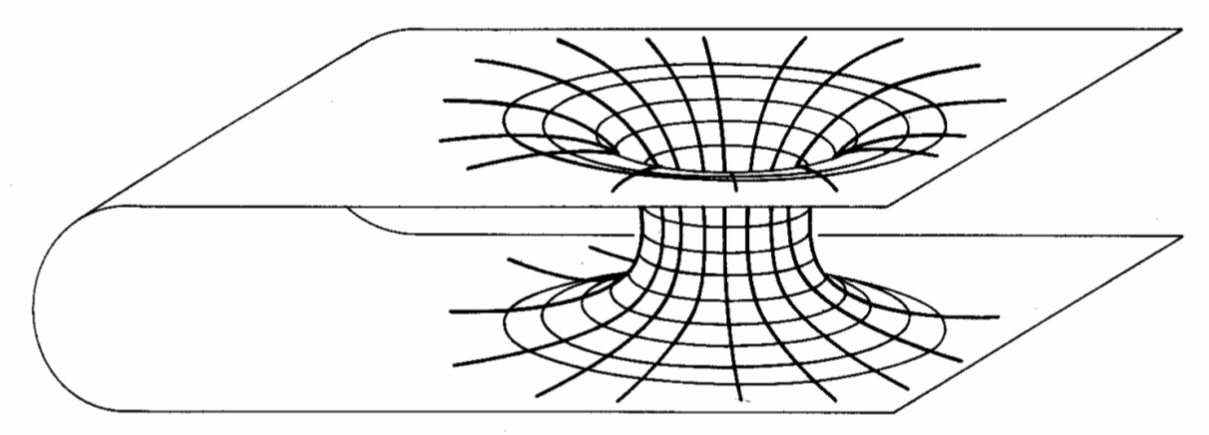
• 图11：连接两个遥远时空区域的史瓦西虫洞

不幸的是，1962年，两位美国物理学家约翰·惠勒和罗伯特·富勒证明，如果施瓦茨子虫洞将同一宇宙的两个部分连接起来，它们会迅速地将任何粒子（包括光子）夹在这两个区域之间（这种虫洞是不稳定的）。

这种不稳定性是由于两个特性造成的：

1. 史瓦西虫洞是有时间依赖性的。虫洞的打开和关闭速度太快，旅行者无法通过。
2. 虫洞咽喉处的潮汐力太强，会杀死旅行者。

其他类型的虫洞

因此，爱因斯坦-罗森桥是不能被穿越的。然而，如果它们的“喉咙”能在外来物质（负质量的物质）存在时保持打开，那么稳定性是可能的。

可穿越虫洞

以下是一个可穿越虫洞应该遵循的几个条件：

1. 虫洞度规应该是静态的（与爱因斯坦-罗森桥相反），并遵循广义相对论场方程
2. 球对称（这将使数学处理更简单）
3. 在连接两个渐近平坦的时空区域的解中一定有一个“喉道”
4. 旅行者在穿过虫洞时所感受到的潮汐力必须足够小

现在让我们根据1988年美国理论物理学家基普·索恩（Kip Thorne）和迈克尔·莫里斯（Michael Morris）的一篇论文，用数学术语来研究一个可穿越的虫洞。

一个具有上述属性的虫洞的简单例子，用史瓦西坐标表示，具有以下线元素：

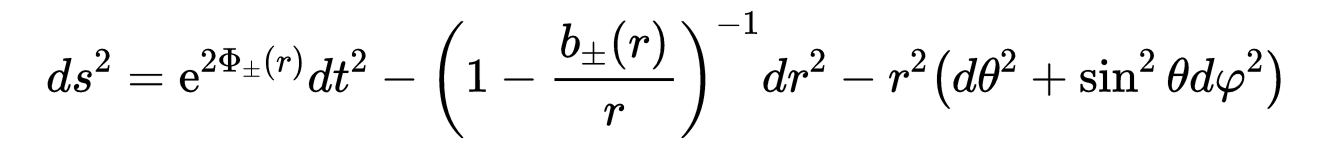
• 式13

所谓的形状函数b(r)决定了虫洞的空间形状。喉道的周长由2πr给出。函数Φ称为红移函数。注意这个度规是与时间无关的。利用爱因斯坦场方程可以计算出虫洞咽道的张力。如果喉道的半径是3千米，喉道的张力等于质量最大的中子星中心的压强！

如果观察者以足够高的速度穿过虫洞的喉咙，他将测量到一个负的质能密度，这违反了所谓的弱能量条件。当考虑到量子效应时，就会出现这种违反的例子。更具体地说，违反行为可能发生在卡西米尔效应的情况下。

换句话说，由于卡西米尔效应，空间某些区域的能量密度可能是负的（相对于普通物质的真空能量）。这一结果使得包括斯蒂芬·霍金在内的许多物理学家认为，这种效应在原则上可以稳定虫洞，使其可穿越。

• 图12：通过虫洞旅行的NASA插图