你可能不知道,现在我们的孩子初高中所学的解析几何知识,都是三百多年前的天才们创立的!。所以,我们还真的不得不感叹,17世纪真的是人类历史上群星璀璨的时代。
我们现在高中课本上所讲的概率论、圆锥曲线等等,其实都和三百多年前一个叫帕斯卡尔的数学家有关。

帕斯卡尔
帕斯卡尔,在有的地方也被翻译为帕斯卡,他在概率论、圆锥曲线等方面的数学成就,也同样沿用至今,成为我们数学史上绕不开的一环。
1623年,帕斯卡尔出生在法国的一个小贵族家庭。说是贵族,其实社会地位也很一般,只是祖上三代在当地的一些政府机构里面做着小差事。但他的父亲却很有学问,和费马有点类似是,帕斯卡尔的父亲不喜欢那些行政和司法工作,偏偏热爱数学,也算是一名业余数学家。
更难能可贵的是,父亲在帕斯卡尔很小的时候就开始亲自充当儿子的家庭教师。[footnoteRef:0]所以,帕斯卡尔小时候实际上是没有上过学的。 [0: 雅克·阿塔利,《帕斯卡尔:改变世界的天才》,上海人民出版社]
大家也都知道,学校里面的教育难免要交一些死记硬背的东西,尤其是欧洲的语言特色导致孩子在启蒙教育阶段,必须得首先学会语法,学了法文,一般还得学拉丁文,这些东西都很枯燥,也很复杂,很容易把孩子的学习欲望给磨灭掉。

18世纪的欧洲贵族
帕斯卡尔的父亲不希望自己的孩子被教育制度摧残,因此呢,他就干脆自己教育孩子读书,培养帕斯卡尔的理解能力,培养他学习和创造知识的欲望。这种教育方式的直接成果就是,催促了17世纪的又一名神童的诞生。
帕斯卡尔12岁的时候,父亲有一次晚上开会回家后,发现帕斯卡尔正坐在地上全神贯注地顶着各种圆、圆角和平行线。父亲就问他在做什么,他风淡云轻地对父亲说,他正在证明三角形三角之和的度数[footnoteRef:1]。三角形的内角和等于180度,这早在古希腊时期,欧几里得就已经得出了这个结论。 [1: 雅克·阿塔利,《帕斯卡尔:改变世界的天才》,上海人民出版社]
但是,帕斯卡尔小小年纪,在没有读过相关的数学作品的情况下,竟然独立地发现了这个”秘密”,这还是让父亲震惊不已。所以,从他12岁开始,父亲就正式地教他学习数学。
从此,帕斯卡尔就对数学产生了更多更大的兴趣。到了1639年,帕斯卡尔受到法国梅尔塞纳科学院的邀请,当着全院院士的面介绍他自己的研究成果。
这份研究成果,就是著名的《圆锥曲线论》。在《圆锥曲线论》里,帕斯卡尔得出一个结论:圆锥曲线内接六边形其三对边的交点为共线。
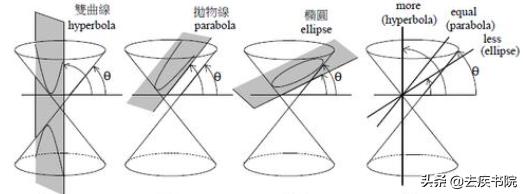
圆锥曲线
这条理论,后来就被我们称为帕斯卡定理。这条定理是什么意思呢?它的意思就是:在任意一个椭圆或者圆形的曲线内部如果有一个六边形的话,那把这个六边形相对应的三组边延长,延长之后三组边之间会得到三个交点,这三个交点就一定是在同一条直线上的。
这个定理有什么作用?其实在我们的生活中并不常用,但在摄影几何里面,运用地会比较多。这里要介绍一下射影几何的概念:射影几何啊,讲得简单一点,就是把立体的东西,通过投影变成平面的东西,我们现代人绘图、测量、航空、摄影,一般都会用到这方面的知识。
大家请注意,这件事发生在1639年,帕斯卡尔才16岁。16岁就做出了这样的成绩,是相当了不起的。
梅尔塞纳科学院在这一年的11月份把帕斯卡尔的研究成果通告给了整个数学界,据说笛卡尔在看到帕斯卡尔的论文之后产生了一股嫉妒之情,笛卡尔觉得16岁的孩子是不可能能搞清楚这个问题的,所以肯定是剽窃。这件事后来也影响到了帕斯卡尔这个晚辈与笛卡尔这位前辈之间的关系。[footnoteRef:2] [2: 雅克·阿塔利,《帕斯卡尔:改变世界的天才》,上海人民出版社]

帕斯卡尔
这算是帕斯卡尔的第一个数学成就。
帕斯卡尔对数学的另外一个贡献体现在概率论上。什么是概率论呢?其实啊,最初的概率论和赌博有关。比如在帕斯卡尔的著作《思想录》里面,就专门有一章是讨论赌博问题的。
在《思想录》里面,帕斯卡尔就有一段特别注明的话:当我们被迫参与赌局的时,必须放弃理智,以求活命,不能为了赢得无限而冒生命危险,如此胜局的几率,与一无所失的几率是一样的。[footnoteRef:3] [3: 帕斯卡尔,《思想录》,中国法制出版社]
这句话的意思就是说,当我们在赌博的时候,不要想着赢得一切。为什么呢?因为赢得一切的概率和输掉一切的概率是一样的。这里其实帕斯卡尔就已经开始把眼光放到了概率上面。
这件事据说和帕斯卡尔的一位朋友有关。话说1651年的某一天,帕斯卡的朋友向他提出了一个问题:现在有两名赌徒在赌博,两个人约定,谁先赢了五局,桌子上的全部赌注就归谁。

十八世纪的欧洲
这两个人玩啊玩啊,赌徒A赢了4局,赌徒B赢了3局,这时候两个人玩累了,不想再继续玩下去了。那么,这桌子上的赌注应该怎么分配呢?
一般情况下,我们都会觉得,那A赢了4局,B赢了3局,那我们就把所有的钱分成七份,A拿7分之4,B拿7分之3不就行了?但帕斯卡尔的这位朋友说这种想法是错的,正确的答案是A拿4分之3,B拿4分之1。
为什么呢?因为假设两个人再玩一局,那A赢下这局的概率是2分之1,输的概率也是2分之1。如果A赢了最后一局,那它就赢了五局,既然赢了五局,那所有的钱都得归他。如果A输了,那B就赢了四局,也就是说,A和B最终都会赢四局。如果A和B都赢了四局,这些钱就应该平分。
现在既然这两个人都不想玩了,那A拿到的钱就应该这么分:首先,赢下下一局把钱全部拿走的概率为1/2,输掉下一局的概率也是1/2,但是,输掉之后实际上两个人都赢四局,那钱就得平分,所以这里平分的概率也是1/2。大家注意,这里有两个1/2,所以其实它的最终平分的概率为1/4。
因此,对于A来说,它赢得比赛的概率为1/2,输掉比赛后钱得对半分,对半分的概率为1/4,两个概率加在一起,总概率为3/4。所以,现在A和B如果不玩这最后一局的话,按照概率,A应该拿走3/4的钱,相应的,B只能拿1/4。[footnoteRef:4] [4: 参考网页”概率论的起源”:https://zhidao.baidu.com/question/1799234028146578027.html]
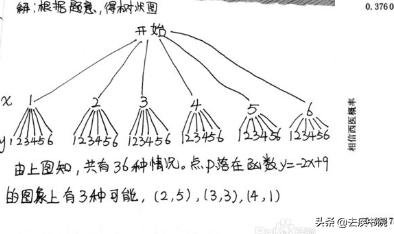
简单的概率问题
帕斯卡尔最开始听到这个故事也觉得有点懵,所以回去之后就思考了两三年。这两三年里,他多次与费马在通信中讨论这个问题,最终把概率的问题给搞懂了。这次对于赌博的讨论,最后也就发展出了数学这么学科中特别重要的分支——概率论。
帕斯卡尔的第三个数学成就和父亲有关。我们之前也说了,帕斯卡尔的父亲在政府部门里面当着一个小吏,所以有时候工作是很辛苦的。帕斯卡尔于是灵机一动,要为父亲设计一个函数计算器。
这台计算器花了帕斯卡尔两年的时间,后来又花了他十年的时间对它进行改良和完善,最后使得这台计算器能够进行8位数的加减乘除。这也是世界上第一台比较实用的计算器,它的模型被保留了下来,经过三百多年的辗转,最终被美国的IBM公司收藏了起来。[footnoteRef:5] [5: 道格拉斯·格鲁秀斯,《帕斯卡尔》,中华书局]
帕斯卡尔的一生都在搞学术,孜孜不倦,除了数学,他还花费了很大的力气去做实验研究气压问题。我们现在高中物理课本里许多关于气压的理论贡献,都是帕斯卡尔做出的。比如我们现在提到”压强”这个概念,都会说压强是多少多少”帕”, “帕”作为一种计量单位,其实使用的就是帕斯卡尔的名字。
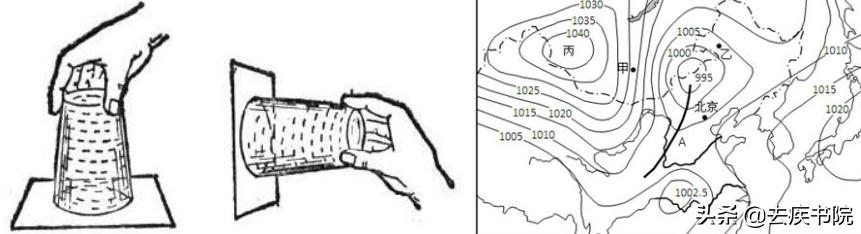
气压
但比较可惜的是,帕斯卡尔39岁就去世了。他的天赋不比费马、笛卡尔以及我们后面要说的牛顿和莱布尼茨差,但是很可惜,从1965年开始他就身患重病,最后一病不起,直至去世。
帕斯卡尔可能不知道,在他身患重病的时候,德国的另一位数学天才莱布尼茨已经成年并且已经显示出对数学的巨大天分。
后来,莱布尼茨阅读了帕斯卡尔的论文手稿,差不多20年之后,莱布尼茨创立了数学史上另一个重要的理论——微积分。是的,莱布尼茨之所以能创立微积分,帕斯卡尔功不可没。
帕斯卡尔死了,但他对数学的贡献还在延续。












